데이터 압축의 개념

압축? Zip 📁파일을 말하는 건가?
Yes, 하지만 우리 일상에 존재하는 압축은 Zip 뿐만이 아니다.
우리는 일상에서 다양한 디지털 컨텐츠를 마주한다.
대표적으로 이미지, 오디오, 비디오 컨텐츠를 예로 들 수 있을 것인데, 이런 컨텐츠의 원본 크기는 어느 정도일까?
| 이미지 (12MP, 24bit RGB) | 36MB |
| 오디오 (24bit/192kHz, stereo) | 70MB/min |
| 비디오 (1080p, RGB, 30fps) | 11GB/min |
생각보다 매우 큰 크기를 자랑하지 않는가? 스트리밍 사이트를 통해 이런 원본 데이터를 이용한다면?
90분의 런타임을 가진 영화 한편 시청에 약 1TB(...)의 데이터 사용량이 필요할 것이다.
이러한 비효율성을 줄이고 싶어 등장한 것이 바로 데이터 압축이다.
데이터 압축
- 디지털 컨텐츠, 혹은 데이터의 용량을 줄이는 기법
- 오디오, 비디오와 같은 컨텐츠의 경우 코덱 CODEC (COder, DECoder)라고 불리기도 한다.
- 데이터를 더 작은 사이즈로 변환하여, 저장 및 전송 효율성을 높이는 것을 목표로 한다.
우리가 일상에서 마주하는 디지털 컨텐츠는 대부분 압축 과정을 거쳐 우리에게 전달된다.
데이터 압축의 종류
데이터 압축은 크게 두 종류로 나눌 수 있다. 그 기준은 압축 과정에서의 정보 손실 여부로 볼 수 있다.
1. 무손실 압축
무손실 압축은 압축된 데이터를 다시 복원했을 때, 원본 데이터와 완벽히 동일하게 복원되는 압축 방식이다.
즉, 압축 및 복원 과정에서 정보의 손실이 없다는 것.
장점
- 원본 데이터와 완벽히 동일하게 복원 가능하므로, 정보의 손실이 없어 신뢰성이 높음. 따라서 문서, 소프트웨어, 데이터베이스 파일 등에 적합하다.
- 일반적으로 압축, 복원 과정의 연산량이 적은 편
단점
- 압축률이 낮을 수 있다. 즉, 데이터 크기의 감소 효과가 그다지 크지 않을 수 있다.
ZIP, RAR 등 범용적인 아카이빙 압축 방식은 데이터가 유실되어선 안되기 때문에, 이러한 무손실 압축 기법을 사용한다.
2. 손실 압축
손실 압축은 압축 과정에서 일부 데이터를 의도적으로 제거한다.
물론 정보의 손실이 없다면 좋겠지만, 의도적으로 일부 데이터를 제거하여 무손실 압축에 비해 비약적으로 높은 압축률을 가질 수 있어 이러한 손실 압축 방식이 널리 사용된다.
장점
- 높은 압축률 : 무손실 압축 대비 데이터의 크기를 대폭 줄일 수 있어, 저장 공간 및 전송 대역폭을 크게 절감할 수 있다.
- 디지털 미디어(음악, 사진, 동영상)에서 주로 활용된다. 사용자 경험에 큰 영향을 주지 않으면서, 전송 및 저장 공간의 효율성을 확보할 수 있기 때문
단점
- 정보 손실 : 압축 해제 후의 데이터는 원본과 동일하지 않음, 손실이 심할 경우엔 사용자가 충분히 인지 가능한 왜곡이나 노이즈가 발생한다.
- 일반적으로 무손실 압축에 비해 연산량이 많은 편이다.
음악, 사진, 동영상과 같은 디지털 컨텐츠는 어느 정도 손실이 일어나도 사용자가 알아채기 어려우며, 전송 대역폭 및 저장 공간의 효율성을 극대화할 수 있기 때문에 손실 압축이 사용되곤 한다.
인간이 이러한 손실을 인지하기 힘들도록, 인간의 감각 특성을 분석하여 실제로 인지하기 어려운 데이터를 제거한다.
데이터 압축의 응용 사례
이미지 🖼️
| 압축 방식 | 포맷 | 특징 |
| 무손실 압축 | PNG, GIF, RAW 등 | 원본 데이터를 그대로 복원할 수 있어, 품질 손실이 허용되지 않는 분야에서 사용 |
| 손실 압축 | JPEG (JPG) 등 | 1. 원본 이미지 대비 파일 크기를 대폭 줄일 수 있다. 2. 인터넷에 떠도는 이미지의 80%가 JPEG 포맷이라고 한다. 3. 디지털 풍화의 주범으로, 손실 압축된 이미지를 다시 손실 압축하여 공유하는 과정이 반복된다면, 이미지의 품질이 심각히 저하될 수 있다. |
오디오 🎵
| 압축 방식 | 포맷 | 특징 |
| 무손실 압축 | FLAC, ALAC 등 | 음질의 손실 없이 원음을 복원할 수 있어, 전문 녹음이나 HIFI 음원 스트리밍 등에서 사용 |
| 손실 압축 | MP3, SBC, AAC, LDAC, aptX 등 | 1. 가청 주파수, 청각적 마스킹 효과 등, 인간의 청각 특성을 이용하여 일부 데이터를 제거하여 압축한다. 낮은 용량으로 인해 스트리밍, 휴대용 기기 등에서 적극 사용된다. 2. AAC의 경우 256kbps 기준, 무손실인 ALAC 대비 최대 24배 작은 용량을 자랑한다. |
비디오 🎬
| 압축 방식 | 포맷 | 특징 |
| 무손실 압축 | HuffYUV 등 | 오디오나 이미지와 다르게 비디오는 압도적으로 큰 용량을 자랑하기 때문에, 압축률이 낮은 무손실 압축의 경우, 일상 생활에서 마주칠 일은 없다고 봐도 무방하다. |
| 손실 압축 | MPEG, H.264 등 | 1. 프레임 간 중복을 활용하여 효율적으로 데이터의 크기를 줄임 2. 유튜브, 넷플릭스 등 많은 스트리밍 사이트는 이러한 손실 압축 기법을 이용하여, 낮은 대역폭에서도 고품질의 영상을 제공한다. |
정보 엔트로피
사건에 대한 불확실성이 높다면 정보량이 많으므로 해당 데이터를 표현하는데 더 많은 비트가 필요하고,
반대로 불확실성이 낮다면 정보량이 더 적으므로 더 적은 비트가 필요할 것이다.
정보 엔트로피는 확률 변수의 불확실성에 대한 척도로 데이터 압축의 핵심 개념 중 하나이다.
하나의 사건에 대한 자기 정보량 I(x)는 다음과 같이 표현될 수 있다.
p(x) := 사건 x가 발생할 확률
I(x) = -log2(p(x))
만약 동전 던지기에서 앞면과 뒷면이 나올 확률이 50%로 동일하다면, 앞뒷면 모두 자기 정보량 I(x) = -log2(0.5) = 1이 될 것이다.
사건들에 대한 평균 엔트로피 H(X)는 다음과 같다.
H(X) = ∑ p(xi) I(xi) = -∑ p(xi) log2(p(xi))
따라서 동전 던지기에서 동전 던지기에서 앞뒷면의 확률이 50%로 동일하다면, 평균 엔트로피는 0.5 x 1 + 0.5 x 1 = 1이다.
하지만 만약 앞면이 90%, 뒷면이 10%의 확률을 가진 편향된 동전이라면? 평균 엔트로피는 0.9 x -log2(0.9) + 0.1 x -log2(0.1) = 0.469이다. 이는 공평한 동전보다 정보의 불확실성이 줄었음을 의미한다.
이러한 정보 엔트로피가 시사하는 바는 다음과 같다.
- 엔트로피를 통해 데이터 압축의 이론적 한계를 이해할 수 있다.
- 압축 알고리즘은 평균 엔트로피에 근접하는 크기를 목표로 설계된다. 이론적으로 평균 엔트로피보다 짧은 비트로 압축할 수 없다.(무손실 압축의 경우)
- 정보가 가지는 불확실성이 낮을 수록, 데이터를 더 효과적으로 압축할 수 있다.
매우 극단적인 예로, 0000이라는 비트 뒤에는 항상 0001이라는 비트가 따라오는 데이터가 있다고 가정해 보자.
0000이라는 비트 뒤는 항상 정해져 있으므로 압축 과정에서 0000 뒤의 0001이라는 비트를 저장할 필요가 없을 것이다.
압축 알고리즘
압축 알고리즘 2가지를 간단하게 소개하고자 한다. 먼저 소개할 RLC(Run-Length Coding)은 데이터 압축 방식에 대한 아주 간단한 알고리즘으로 압축에 대한 이해를 도울 수 있다. 두 번째로 소개할 허프만 코딩(Huffman Coding)은 실제 현대 압축 코덱에서도 널리 활용되는 매우 재미있는 알고리즘이다.
RLC (Run-Length Coding)
매우 간단하고 직관적인 압축 기법으로, 연속되는 데이터를 횟수 + 데이터로 표현하여, 데이터의 중복을 줄일 수 있다. 단색 영역이 많은 이미지(만화, 애니메이션 등)와 같이 연속된 값이 많은 데이터에 사용될 수 있겠으나, 실제로 응용되는 경우는 많지 않다.
AAAABBBBBCDD라는 원본 데이터가 있다고 하자. 연속되는 데이터를 횟수와 데이터로 표현하여 압축하면 결과는 다음과 같을 것이다.
원본 데이터 : AAAABBBBBCDD
A = 4번, B = 5번, C = 1번, D = 2번 연속됨
압축 데이터 : 4A5B1C2D
원본 데이터의 길이는 12인 반면, 압축 데이터의 길이는 8로, 2/3 크기로 압축된 것을 확인할 수 있다.
허프만 코딩 (Huffman Coding)
1952년 등장하여, 현대까지 여러 압축 코덱에 응용되고 있는 전설적인 압축 알고리즘 중 하나이다.
데이터의 문자 혹은 기호의 등장 빈도에 따라 다른 길이의 코드를 부여하여 압축하는 기법(가변 길이 코드)이다.
출현 빈도가 높은 문자의 경우 적은 비트의 코드로 변환, 반대로 출현 빈도가 낮은 문자의 경우 비교적 긴 길이의 코드로 변환하여 전체 데이터를 표현하는데 필요한 비트 수를 줄이는 기법이다.
알고리즘은 다음과 같다. (구현에 따라 세부 방식이 다를 수 있다. 핵심은 출현 빈도에 반비례하는 길이의 코드 부여)
- 빈도 계산 : 입력 데이터에서 각 문자의 등장 횟수를 계산한다.
- 트리 구성 : 내림차순으로 정렬 후, 가장 낮은 빈도의 두 기호를 선택해 하나의 노드로 합치는 과정을 반복하여 최종적으로 하나의 트리를 만든다.
- 코드 할당 : 트리의 루트로부터 각 리프 노드에 이르는 경로를 따라 왼쪽이면 0, 오른쪽이면 1을 할당하여, 각 문자에 코드를 부여한다.
예를 들어, ABAABBBBACDDDEE라는 원본 데이터가 있다고 가정하자.
원본 데이터 : ABAABBBBACDDDEE
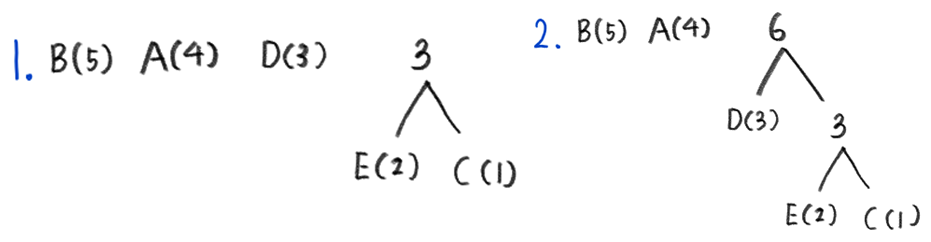

트리가 완성되었으니 3번 과정인 코드 할당을 거쳐 각 문자에 코드를 할당한다. 깊이 우선 탐색을 이용해 각 문자에 해당하는 코드를 얻을 수 있을 것이다.
A = 01, B = 00, C = 111, D = 10, E = 110
이를 대입한 압축된 데이터는
압축된 데이터 : 010001010000000001111101010110110
원본 데이터에서 문자당 1Byte라고 하면, 원본데이터의 크기는 15Byte = 120Bit이다.
반면 압축된 데이터는 33Bit이다. 대략 1/4 크기만큼 압축된 것을 확인할 수 있다.
또한 허프만 코딩은 접두사 코드이다. 즉, 한 코드가 다른 코드의 접두사에 해당하는 경우가 없기 때문에, 압축된 데이터의 각 문자 사이에 구분자가 없어도 문자를 구분할 수 있다는 용이함이 있다.
지금까지 데이터 압축에 대해 간단히 알아보았다.
불필요한 부분은 덜어내고 중요한 부분만 남기는 손실 압축 코덱처럼,
오늘 하루의 근심과 걱정은 덜어내고 즐거움과 행복만 간직하시길 바랍니다.